L'analyse prédictive permet aux organisations de prévoir les événements futurs en tirant parti des données passées. Lorsque l'on se lance dans ce travail, surtout d'un point de vue de Minimum Viable Product (MVP), un outil simplifié mais robuste est essentiel, et j'aime commencer avec Scikit-Learn. C'est mon terrain de jeu initial pour l'exploration de l'analyse prédictive.

Aperçu de l'analyse prédictive

Lors d'un récent atelier - "Identifying Opportunities to Leverage AI Within the Manufacturing Sector", nous avons exploré la capacité de l'IA à transformer le domaine manufacturier. Bien que la discussion se soit principalement concentrée sur la fabrication, les connaissances sont applicables à de nombreux secteurs.

Fondamentalement, l'analyse prédictive est un outil agnostique du domaine qui est utile dans tous les domaines, de la santé à la finance en passant par la vente au détail et au-delà.

L'essence de l'analyse prédictive réside dans l'utilisation de données historiques associées à l'IA et à l'apprentissage automatique pour prédire les résultats futurs. Cette prévoyance facilite la prise de décisions stratégiques, minimise les risques et réduit les coûts d'arrêt en signalant les blocages potentiels et les problèmes. Cela nous permet d'optimiser les opérations et de maximiser les profits.

Quelques exemples d'applications :

• Manufacturier: Utilisation de la maintenance prédictive pour réduire les temps d'arrêt des machines.
• Santé: Augmentation du diagnostic précoce et de l'évaluation des risques de maladies.
• FinTech: Renforcement de la détection de la fraude et de l'évaluation du risque de crédit.

Un avantage supplémentaire de l'analyse prédictive réside dans sa transférabilité ; nous pouvons emprunter des stratégies d'un domaine pour apporter de l'innovation à un autre.

Du problème au déploiement du MVP

Passer d'un énoncé de problème à un MVP comprend :

1. Un aperçu du problème pour des insights exploitables
2. .L'acquisition, le nettoyage, la transformation et la structuration des données.
3. La construction et la validation du modèle.
4. Le réglage fin des modèles pour les aligner sur le contexte.

Je crois que les personnes, le processus et le produit forment la base de l'innovation technique. Nous pouvons construire de grandes solutions en commençant toujours par une question et une compréhension approfondie du contexte, des récits d'utilisateurs et des parties prenantes.

Scikit-Learn: le MVP

Bien que de nombreux outils et plateformes soient disponibles pour l'analyse prédictive, Scikit-Learn se distingue par sa simplicité, sa facilité d'utilisation et son efficacité, ce qui en fait mon choix préféré pour les MVP et les projets de preuve de concept. C'est une bibliothèque qui abaisse la barrière à l'entrée, rendant l'étape initiale de modélisation prédictive moins intimidante et plus structurée.

Le bénéfice de Scikit-Learn réside dans sa courbe d'apprentissage douce, qui est utile pour les personnes ayant une compréhension fondamentale de Python. Il possède une API bien organisée, cohérente et intuitive qui accélère l'intégration. De plus, il dispose d'une riche bibliothèque d'algorithmes pour diverses tâches d'apprentissage automatique, offrant une plateforme robuste pour construire, expérimenter et itérer sur des modèles prédictifs. La conception modulaire favorise l'extensibilité et l'interopérabilité avec d'autres bibliothèques, renforçant son attrait pour le développement de MVP. La nature simple mais puissante de Scikit-Learn en fait un excellent choix pour le prototypage rapide, accélérant le processus du concept à un modèle fonctionnel, prêt pour une validation réelle.

‍

Dimensions du problème

L'analyse prédictive tourne généralement autour de la classification (catégorisation des données) ou de la régression (prévision de valeurs continues) :

• Classification : Catégorisation des données lorsque la variable de résultat appartient à un ensemble prédéfini (par exemple, 'Oui' ou 'Non').
• Régression : Prévision de valeurs continues lorsque la variable de résultat est réelle ou continue (par exemple, poids ou prix).

Exemple pratique : Analyse de la progression du diabète

Illustrons cela avec un exemple pratique en utilisant un ensemble de données de santé sur la progression du diabète. Grâce à Scikit-Learn, l'accès à un ensemble de données fictives sur le diabète est simple. Cet ensemble de données contient dix variables telles que l'âge, l'IMC et les mesures de sérum sanguin pour plus de 400 patients diabétiques.

Nous cherchons à répondre aux histoires utilisateur suivantes :

• Cadre de santé : Rationalisation de l'admission des patients pour une intervention rapide.
• Médecin : Identification des facteurs contribuant à une prédiction précise de la progression du diabète.
• Patient : Utilisation des mesures de santé pour comprendre et potentiellement atténuer les risques de progression du diabète.

import pandas as pdfrom sklearn import datasets# Load the diabetes datasetdiabetes = datasets.load_diabetes()data = pd.DataFrame(data=diabetes.data, columns=diabetes.feature_names)data["target"] = diabetes.target

Analyse préliminaire et construction du modèle

Avant de se lancer dans la construction du modèle, il est crucial de réaliser une analyse exploratoire. Cela révèle souvent des insights qui guident le choix des modèles prédictifs et des caractéristiques..

import matplotlib.pyplot as pltimport seaborn as sns# Display the first few rows of the datasetdata.head()# Summary statisticsdata.describe()# Correlation matrixplt.figure(figsize=(10, 8))sns.heatmap(data.corr(), annot=True)plt.show()

La matrice de corrélation affiche les relations entre diverses caractéristiques et la variable cible dans l'ensemble de données sur le diabète. Voici les principaux insights de la matrice de corrélation :

Corrélation entre l'IMC et la cible :

• Il y a une corrélation positive entre l'IMC (indice de masse corporelle) et la variable cible, ce qui suggère qu'à mesure que l'IMC augmente, la mesure du diabète a tendance à augmenter également.

Corrélation entre la pression artérielle (bp) et la cible :

• La pression artérielle montre une corrélation positive avec la variable cible. Cela indique que des valeurs de pression artérielle plus élevées sont associées à des mesures de diabète plus élevées.

Negative Correlation of S3 and Target:

• S3 présente une corrélation négative avec la variable cible, indiquant que des valeurs plus élevées de S3 sont associées à des valeurs plus faibles de la mesure du diabète.

Corrélation entre les caractéristiques :

• Les caractéristiques S1 et S2 présentent une corrélation positive élevée, indiquant une forte relation linéaire entre elles.
• S4 et S3 ont une forte corrélation négative, montrant que lorsque une variable augmente, l'autre a tendance à diminuer significativement.
• Les paires S4 et S2 et S4 et S5 présentent également de fortes corrélations positives, suggérant que ces caractéristiques se déplacent probablement ensemble.

Corrélation avec l'âge :

• L'âge présente une corrélation positive avec diverses caractéristiques, notamment la pression artérielle (bp), S5 et S6, et une corrélation positive moins significative mais encore importante avec la variable cible. Ces insights donnent un aperçu de la manière dont diverses variables physiologiques et de test se rapportent les unes aux autres et à la mesure du diabète, ce qui pourrait être crucial pour le développement de modèles prédictifs ou la compréhension des motifs sous-jacents dans l'ensemble de données.

‍

Prétraitement des données

Le prétraitement des données est vital dans la construction d'un modèle d'apprentissage automatique car il prépare les données brutes à être introduites dans le modèle, assurant ainsi de meilleures performances et des prédictions plus précises. Dans ce processus, la standardisation des données et leur séparation en ensembles d'entraînement et de test sont des étapes essentielles.

Le premier objectif ici est d'avoir des ensembles de données séparés pour l'entraînement et l'évaluation du modèle. Une règle générale commune est la règle des 80-20, où 80 % des données sont utilisées pour l'entraînement et les 20 % restants pour le test. Ce ratio offre un bon équilibre, garantissant que le modèle dispose de suffisamment de données pour apprendre tout en ayant encore une quantité substantielle de données non vues pour l'évaluation.

Deuxièmement, la standardisation est cruciale pour de nombreux algorithmes d'apprentissage automatique, en particulier les algorithmes basés sur la distance et les algorithmes basés sur la descente de gradient. Elle met à l'échelle les données pour avoir une moyenne de 0 et un écart type de 1, garantissant ainsi que toutes les caractéristiques contribuent également au calcul des distances ou des gradients.

‍

from sklearn.model_selection import train_test_splitfrom sklearn.preprocessing import StandardScaler# Splitting the data into training and testing setsX = data.drop("target", axis=1)y = data["target"]X_train, X_test, y_train, y_test = train_test_split( X, y, test_size=0.2, random_state=42)# Standardize the datascaler = StandardScaler()X_train = scaler.fit_transform(X_train)X_test = scaler.transform(X_test)

Construction du modèle - Régression linéaire

La régression linéaire est une première étape simple en analyse prédictive en raison de sa simplicité et de sa facilité d'interprétation. Elle fonctionne sous l'apprentissage supervisé, établissant une relation linéaire entre les caractéristiques d'entrée et la variable cible.

from sklearn.linear_model import LinearRegression# Create and train the modellr = LinearRegression()lr.fit(X_train, y_train)

La simplicité de la régression linéaire réside à la fois dans sa commande d'entraînement en une seule ligne et dans sa sortie de modèle, qui est facile à interpréter. Les coefficients nous indiquent le poids ou l'importance de chaque caractéristique, tandis que l'interception nous donne une prédiction de référence lorsque toutes les valeurs des caractéristiques sont nulles. Cette interprétabilité fait de la régression linéaire un excellent point de départ pour la construction de modèles et un outil précieux pour communiquer les résultats aux parties prenantes.

Évaluation et visualisation des résultats

Évaluer les performances d'un modèle consiste à comprendre sa précision et à identifier les domaines d'amélioration. Une métrique standard utilisée dans les tâches de régression est l'erreur quadratique moyenne (MSE), qui quantifie la différence moyenne au carré entre les valeurs réelles et prédites. Une valeur de MSE plus faible indique un meilleur ajustement du modèle aux données, bien qu'il soit important de noter que le MSE est sensible aux valeurs aberrantes.

Visualiser la relation entre les valeurs réelles et prédites éclaire davantage les performances du modèle. Un graphique de dispersion est un outil pratique à cet effet, représentant clairement à quel point les prédictions de notre modèle correspondent aux valeurs réelles. Plus les points se regroupent autour de la ligne d'identité (une ligne avec une pente de 1, passant par l'origine), meilleure est la capacité de notre modèle à faire des prédictions précises.

‍

from sklearn.metrics import mean_squared_errorimport numpy as np# Predictionsy_pred = lr.predict(X_test)# Calculating and displaying the Mean Squared Errormse = mean_squared_error(y_test, y_pred)print(f"Mean Squared Error: {mse}")# Visualizing the actual values and predicted valuesplt.scatter( y_test, y_pred, alpha=0.5)  # Added alpha for better visualization if points overlapplt.xlabel("Actual values")plt.ylabel("Predicted values")plt.title("Actual values vs Predicted values")# Adding line of identitylims = [ np.min([plt.xlim(), plt.ylim()]),  # min of both axes np.max([plt.xlim(), plt.ylim()]),]  # max of both axes# now plot both limits against each otherplt.plot(lims, lims, color="red", linestyle="--")plt.xlim(lims)plt.ylim(lims)plt.show()

Dans cette visualisation, la ligne rouge en pointillés représente la ligne d'identité, où un modèle parfait aurait tous les points. Les écarts par rapport à cette ligne indiquent des erreurs de prédiction. Un tel outil visuel fournit un aperçu qualitatif des performances du modèle. Il sert d'outil d'explication tangible pour les parties prenantes, montrant les forces du modèle et les domaines nécessitant des améliorations dans un format digestible.

Passer à un problème de classification

Notre première approche utilisait un modèle de régression linéaire pour prédire la variable cible continue représentant la progression du diabète. Cependant, comme évalué par l'erreur quadratique moyenne, les performances du modèle ont encore de la marge d'amélioration.

Transformer le problème en un scénario de classification binaire apporte souvent une perspective différente et pourrait conduire à de meilleures performances. Dans certains cas, en le transformant en un problème de classification binaire, nous cherchons à prédire si le diabète d'un patient a progressé en fonction d'un seuil prédéfini.

Définissons la progression comme une variable binaire : 1 si la mesure de progression est supérieure à un certain seuil et 0 sinon. Nous choisirons la médiane de la variable cible dans l'ensemble d'entraînement comme seuil pour la simplicité :

pythonfrom sklearn.preprocessing import Binarizer# Defining the thresholdthreshold = np.median(y_train)# Transforming the target variablebinarizer = Binarizer(threshold=threshold)y_train_class = binarizer.transform(y_train.values.reshape(-1, 1))y_test_class = binarizer.transform(y_test.values.reshape(-1, 1))

Nous pouvons maintenant procéder avec un modèle de classification, maintenant que nous avons notre variable cible binaire. Un choix courant pour de tels problèmes est la régression logistique :

from sklearn.linear_model import LogisticRegression# Training the Logistic Regression modellr_class = LogisticRegression()lr_class.fit(X_train, y_train_class.ravel())# Making predictions on the test sety_pred_class = lr_class.predict(X_test)

Évaluer le modèle

Après l'entraînement, évaluer le modèle sur des données non vues est essentiel pour évaluer ses performances et sa robustesse. Scikit-Learn fournit divers outils, notamment un rapport de classification et une matrice de confusion, qui sont utilisés pour les problèmes de classification. À travers ces métriques, nous pouvons comprendre la précision du modèle, le taux de mauvaise classification et d'autres indicateurs de performance cruciaux.

Rapport de classification

Le rapport de classification fournit les principales métriques suivantes pour chaque classe et leurs moyennes :

• Précision : Le rapport des observations positives correctement prédites au total des prédictions positives. Une précision élevée est liée à un faible taux de faux positifs.
• Rappel (Sensibilité) : Le rapport des observations positives correctement prédites au total des observations dans la classe réelle. Il nous dit quelle proportion de la classe positive réelle a été identifiée correctement.
• ‍F1-Score : La moyenne pondérée de Précision et de Rappel.
• Support : Le nombre d'occurrences réelles de la classe dans l'ensemble de données spécifié.

from sklearn.metrics import classification_report# Evaluating the modelclass_report = classification_report(y_test_class, y_pred_class)print(class_report)

           precision    recall  f1-score   support         0.0       0.77      0.82      0.79        49         1.0       0.76      0.70      0.73        40    accuracy                           0.76        89   macro avg       0.76      0.76      0.76        89weighted avg       0.76      0.76      0.76        89

Matrice de confusion

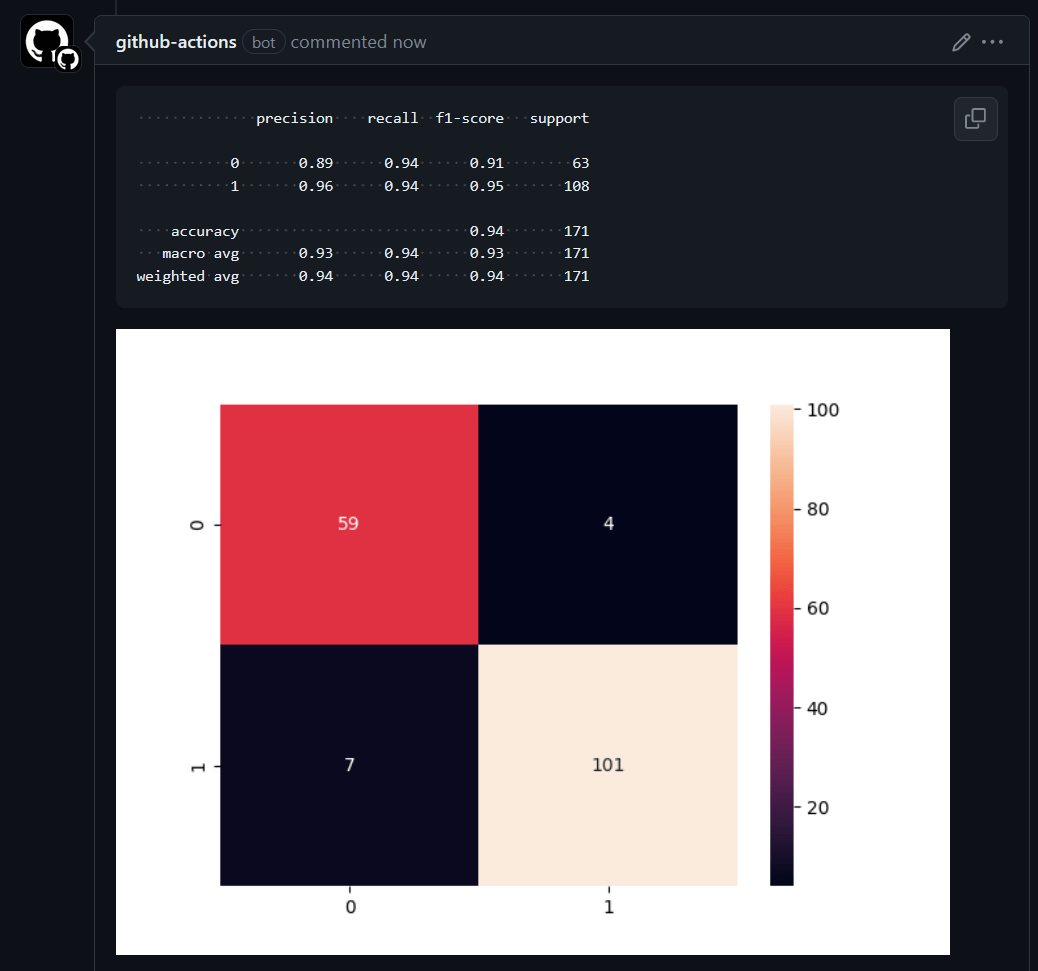
Une matrice de confusion est une table utilisée pour évaluer les performances d'un modèle de classification. Elle donne non seulement un aperçu des erreurs commises par un classificateur, mais aussi les types d'erreurs qui se produisent. Dans une matrice de confusion binaire, les éléments diagonaux représentent le nombre de prédictions correctes pour chaque classe, tandis que les éléments hors diagonale représentent les erreurs de classification.

from sklearn.metrics import ConfusionMatrixDisplaydisp = ConfusionMatrixDisplay.from_estimator( lr_class, X_test, y_test_class, display_labels=["Not Progressed", "Progressed"], cmap=plt.cm.Blues,)plt.show()

Dans cette visualisation, chaque colonne de la matrice représente les instances dans une classe prédite, tandis que chaque ligne représente les instances dans une classe réelle. L'étiquette "Non Progressé" est associée à 0 et "Progressé" à 1. Les éléments diagonaux représentent le nombre de points pour lesquels l'étiquette prédite est égale à l'étiquette réelle, tandis que les éléments hors diagonale sont ceux que le modèle classe incorrectement.

Cette matrice colorée représente les performances du classificateur, où les teintes plus foncées représentent des valeurs plus élevées. Ainsi, la diagonale serait nettement plus sombre pour un modèle performant que le reste de la matrice.

Réduction de la Dimensionnalité et Visualisation

n Analyse Prédictive, nos modèles travaillent souvent avec de nombreuses dimensions, chacune représentant une caractéristique de données différente. Cependant, naviguer dans un espace de haute dimensionnalité est délicat et peu intuitif. C'est là que des techniques de réduction de dimensionnalité comme t-SNE (t-Distributed Stochastic Neighbor Embedding) entrent en jeu, agissant comme un pont de la haute dimensionnalité à une représentation visuelle, souvent en 2 dimensions.

Visualiser des données de haute dimensionnalité dans un espace de dimension inférieure, comme 2D, aide à comprendre la distribution des données et les limites de décision du modèle.

from sklearn.manifold import TSNE# Create a TSNE instancetsne = TSNE(n_components=2, random_state=42)# Fit and transform the datatransformed_data = tsne.fit_transform(X_test)# Visualizing the 2D projection with color-codingplt.scatter( transformed_data[:, 0], transformed_data[:, 1], c=np.squeeze(y_test_class), cmap="viridis", alpha=0.7,)plt.xlabel("Dimension 1")plt.ylabel("Dimension 2")plt.title("2D TSNE")plt.colorbar(label="Progressed (1) vs Not Progressed (0)")plt.show()

Le nuage de points coloré produit dans le code ci-dessus montre comment la progression du diabète (catégorisée comme Progressée et Non Progressée) est distribuée dans deux dimensions. Chaque point représente un patient, et la couleur indique le statut de progression. Cette visualisation peut révéler des clusters de points de données similaires, des valeurs aberrantes ou des motifs qui pourraient être corrélés avec les performances du modèle prédictif.

Cette visualisation en 2D pourrait révéler des relations cachées entre les caractéristiques et la variable cible ou entre les caractéristiques elles-mêmes. De telles informations peuvent guider davantage l'ingénierie des caractéristiques, la sélection du modèle ou l'ajustement des hyperparamètres pour améliorer éventuellement la puissance prédictive du modèle.

De telles visualisations peuvent également être un puissant outil de communication lors de la discussion du modèle et des données avec des parties prenantes non techniques. Elle encapsule des relations complexes et de haute dimensionnalité dans une forme simple et interprétable, rendant la conversation sur les décisions du modèle plus accessible.

Récapitulatif

Cette démonstration montre comment passer rapidement d'un problème du monde réel à un simple MVP en utilisant Scikit-Learn pour l'analyse prédictive. Le parcours de la compréhension du problème, du prétraitement des données, de la construction et de l'évaluation des modèles, à la visualisation des résultats est rempli d'apprentissage à chaque étape. Avec des outils simples mais puissants comme Scikit-Learn, l'analyse prédictive est accessible à toutes les parties prenantes.

"